In the table below the check marks indicate all languages spoken by five people: Paula, Quentin, Robert, Sally and Terence. For example, Paula speaks only Chinese and English.
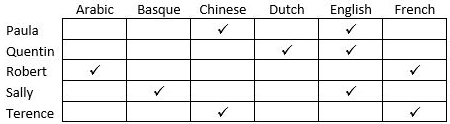
These five people form three teams, Team 1, Team 2 and Team 3. Each team has either 2 or 3 members. A team is said to speak a particular language if at least one of its members speak that language.
The following facts are known.
- Each team speaks exactly four languages and has the same number of members.
- English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team.
- None of the teams include both Quentin and Robert.
- Paula and Sally are together in exactly two teams.
- Robert is in Team 1 and Quentin is in Team 3.
Question 1 : Who among the following four is not a member of Team 2?
- Sally
- Paula
- Quentin
- Terence
EXPLANATION
Answer 3
We can represent each person and the language they speak using the first letter of their name. For instance, English is represented as “E.”
From the given points (1) and (2), we know that each team has three members, and they collectively speak exactly four languages. Since English (E) and another language (C) are spoken by all the teams, either P or T (the only two who can speak C) must be in each team.
Based on point 5), we know that R is in Team 1, and Q is in Team 3. P and S are together in exactly two teams.
If P and S are in Team 1, then the three members of Team 1 would be P, S, and R, and they could collectively speak 5 languages (all except D), making it impossible to form a team. The same issue arises if R, S, and T are in a team.
Hence, P and S must be in Teams 2 and 3, and R, P, and T must be in Team 1.
Here is a table representing the team formations and the languages they collectively speak:
| Team | Members | Languages |
|---|---|---|
| Team 1 | R, P, T | A, F, C, E |
| Team 2 | P, S, T | C, E, B, F |
| Team 3 | Q, P, S | D, E, C, B |
Question 2 : Who among the following four people is a part of exactly two teams?
- Sally
- Quentin
- Robert
- Paula
EXPLANATION
ANSWER D
We can represent each person and the language they speak using the first letter of their name. For instance, English is represented as “E.”
From the given points (1) and (2), we know that each team has three members, and they collectively speak exactly four languages. Since English (E) and another language (C) are spoken by all the teams, either P or T (the only two who can speak C) must be in each team.
Based on point 5), we know that R is in Team 1, and Q is in Team 3. P and S are together in exactly two teams.
If P and S are in Team 1, then the three members of Team 1 would be P, S, and R, and they could collectively speak 5 languages (all except D), making it impossible to form a team. The same issue arises if R, S, and T are in a team.
Hence, P and S must be in Teams 2 and 3, and R, P, and T must be in Team 1.
Here is a table representing the team formations and the languages they collectively speak:
| Team | Members | Languages |
|---|---|---|
| Team 1 | R, P, T | A, F, C, E |
| Team 2 | P, S, T | C, E, B, F |
| Team 3 | Q, P, S | D, E, C, B |
Question 3 : Who among the five people is a member of all teams?
- No one
- Terence
- Sally
- Paula
EXPLANTION
ANSWER:D
We can represent each person and the language they speak using the first letter of their name. For instance, English is represented as “E.”
From the given points (1) and (2), we know that each team has three members, and they collectively speak exactly four languages. Since English (E) and another language (C) are spoken by all the teams, either P or T (the only two who can speak C) must be in each team.
Based on point 5), we know that R is in Team 1, and Q is in Team 3. P and S are together in exactly two teams.
If P and S are in Team 1, then the three members of Team 1 would be P, S, and R, and they could collectively speak 5 languages (all except D), making it impossible to form a team. The same issue arises if R, S, and T are in a team.
Hence, P and S must be in Teams 2 and 3, and R, P, and T must be in Team 1.
Here is a table representing the team formations and the languages they collectively speak:
| Team | Members | Languages |
|---|---|---|
| Team 1 | R, P, T | A, F, C, E |
| Team 2 | P, S, T | C, E, B, F |
| Team 3 | Q, P, S | D, E, C, B |
Question 4 : Apart from Chinese and English, which languages are spoken by Team 1?
- Basque and French
- Arabic and French
- Basque and Dutch
- Arabic and Basque
EXPLANATION
ANSWER 2
We can represent each person and the language they speak using the first letter of their name. For instance, English is represented as “E.”
From the given points (1) and (2), we know that each team has three members, and they collectively speak exactly four languages. Since English (E) and another language (C) are spoken by all the teams, either P or T (the only two who can speak C) must be in each team.
Based on point 5), we know that R is in Team 1, and Q is in Team 3. P and S are together in exactly two teams.
If P and S are in Team 1, then the three members of Team 1 would be P, S, and R, and they could collectively speak 5 languages (all except D), making it impossible to form a team. The same issue arises if R, S, and T are in a team.
Hence, P and S must be in Teams 2 and 3, and R, P, and T must be in Team 1.
Here is a table representing the team formations and the languages they collectively speak:
| Team | Members | Languages |
|---|---|---|
| Team 1 | R, P, T | A, F, C, E |
| Team 2 | P, S, T | C, E, B, F |
| Team 3 | Q, P, S | D, E, C, B |











