CAT 2022 QA Slot 1 | Modern Math – Permutation & Combination CAT Question
The number of ways of distributing 20 identical balloons among 4 children such that each child gets some balloons but no child gets an odd numbe of balloons, is
EXPLANATION
There are 84 number different ways to distribute 20 identical balloons among 4 kids.
Given that,
We must determine how many different ways there are to distribute 20 identical balloons among 4 children so that each child receives some balloons but none of them receive an odd number.
We know that,
Let the quantity of balloons distributed to each kids be 2a, 2b, 2c, and 2d.
2a+ 2b+ 2c+ 2d = 20
So,
a+ b+ c+ d = 10
Each of them get more than one balloons,
So,
Total number of ways= =
=
= 84 ways.
Therefore, There are 84 number different ways to distribute 20 identical balloons among 4 kids.
CAT 2022 QA Slot 2 | Modern Math – Permutation & Combination CAT Question
The number of integers greater than 2000 that can be formed with the digits 0, 1, 2, 3, 4, 5, using each digit at most once, is
(a) 1200
(b) 1420
(c) 1440
(d) 1480
EXPLANATION
Given, we need to find the number of integers greater than 2000 that can be formed with the digits 0, 1, 2, 3, 4, 5, using each digit at most once. Approach: We can form the integers in the following way: – For integers between 2000 and 2999: We can select any of the 6 digits for the thousands place (since 0 cannot be the first digit), and any of the remaining 5 digits for the hundreds place, any of the remaining 4 digits for the tens place, and any of the remaining 3 digits for the units place. Thus, we have 6 × 5 × 4 × 3 = 360 integers in this range. – For integers between 3000 and 4999: We can select any of the 4 digits other than 0 for the thousands place, any of the remaining 5 digits for the hundreds place, any of the remaining 4 digits for the tens place, and any of the remaining 3 digits for the units place. Thus, we have 4 × 5 × 4 × 3 = 240 integers in this range. – For integers between 5000 and 5999: We can select any of the 2 digits other than 0 for the thousands place, any of the remaining 5 digits for the hundreds place, any of the remaining 4 digits for the tens place, and any of the remaining 3 digits for the units place. Thus, we have 2 × 5 × 4 × 3 = 120 integers in this range. Therefore, the total number of integers greater than 2000 that can be formed with the digits 0, 1, 2, 3, 4, 5, using each digit at most once is 360 + 240 + 120 = 720 + 720 = 1440. Hence, the correct answer is option B, 1440.
CAT 2022 QA Slot 3 | Modern Math – Permutation & Combination CAT Question
The arithmetic mean of all the distinct numbers that can be obtained by rearranging the digits in 1421, including itself, is
(a) 2222
(b) 2592
(c) 2442
(d) 3333
EXPLANATION

CAT 2021 QA Slot 1 | Modern Math – Permutation & Combination CAT Question
The number of groups of three or more distinct numbers that can be chosen from 1, 2, 3, 4, 5, 6, 7 and 8 so that the groups always include 3 and 5 while 7 and 8 are never included together is
EXPLANATION
The given problem requires us to determine the number of groups of three or more distinct numbers that can be chosen from the set {1, 2, 3, 4, 5, 6, 7, 8} under certain conditions. Let’s break down the problem into smaller components to arrive at the solution. Step 1: Identify the total number of groups that include 3 and 5 Since the groups must always include 3 and 5, we can fix these two numbers and then select one more number from the remaining six. This can be done in 6 ways. So, there are a total of 6 groups that include 3 and 5. Step 2: Determine the number of groups where 7 and 8 are included together We need to find the number of groups where 7 and 8 are present together. We can select 7, 8, and one more number from the remaining six. This can be done in 6 ways. Therefore, there are a total of 6 groups where 7 and 8 are included together. Step 3: Calculate the number of groups with 3, 5, and without 7 and 8 To find the number of groups with 3, 5, and without 7 and 8, we need to subtract the number of groups where 7 and 8 are included together from the total number of groups that include 3 and 5. Therefore, the number of groups with 3, 5, and without 7 and 8 is 6 – 6 = 0. Step 4: Find the number of groups with 3, 5, and at least one more number The problem states that the groups must have three or more distinct numbers. Since we have already determined that there are no groups with only three numbers, we need to calculate the number of groups with 3, 5, and at least one more number. This can be done by subtracting the number of groups with 3, 5, and without 7 and 8 from the total number of groups that include 3 and 5. Therefore, the number of groups with 3, 5, and at least one more number is 6 – 0 = 6. Step 5: Calculate the number of groups with more than three numbers To find the number of groups with more than three numbers, we need to subtract the number of groups with exactly three numbers from the total number of groups with 3, 5, and at least one more number. Since we have already determined that there are 6 groups with exactly three numbers, the number of groups with more than three numbers is 6 – 6 = 0. Step 6: Determine the final answer Finally, to calculate the total number of groups of three or more distinct numbers, we need to add the number of groups with exactly three numbers to the number of groups with more than three numbers. Therefore, the final answer is 6 + 0 = 6. Therefore, the correct answer is 6.
CAT 2021 QA Slot 2 | Modern Math – Permutation & Combination CAT Question
The number of ways of distributing 15 identical balloons, 6 identical pencils and 3 identical erasers among 3 children, such that each child gets at leas four balloons and one pencil, is
EXPLANATION
Let’s first distribute the balloons to the children. Since each child must get at least 4 balloons, let’s give 4 balloons to each child first. Now we have 3 balloons left to distribute. We can use the stars and bars method to distribute these remaining balloons.
We have 3 children and 3 balloons left, so we can represent the distribution of balloons using 2 bars. For example, if we represent the distribution as **|*|, it means that the first child gets 6 balloons, the second child gets 5 balloons, and the third child gets 4 balloons.
Using this method, we can distribute the balloons in (3+2-1)C(2-1) = 4C1 = 4 ways.
Now we need to distribute the pencils and erasers. Each child must get at least one pencil, so let’s give one pencil to each child first. Now we have 3 pencils and 3 erasers left to distribute. We can use the stars and bars method again to distribute these remaining pencils and erasers.
We have 3 children and 3 pencils left, so we can represent the distribution of pencils using 2 bars. For example, if we represent the distribution as **|*|, it means that the first child gets 2 pencils, the second child gets 1 pencil, and the third child gets 0 pencils.
Using this method, we can distribute the pencils in (3+2-1)C(2-1) = 4C1 = 4 ways.
Similarly, we have 3 children and 3 erasers left, so we can represent the distribution of erasers using 2 bars. Using this method, we can distribute the erasers in (3+2-1)C(2-1) = 4C1 = 4 ways.
Therefore, the total number of ways to distribute the balloons, pencils, and erasers is:
4 x 4 x 4 = 64.
So, there are 64 ways to distribute the balloons, pencils, and erasers among the 3 children such that each child gets at least 4 balloons and 1 pencil.
CAT 2021 QA Slot 3 | Modern Math – Permutation & Combination CAT Question
A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digi numbers is
EXPLANATION

CAT 2020 QA Slot 2 | Modern Math – Permutation & Combination CAT Question
How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3?
EXPLANATION
Consider four blanks – – – – 7 is in thousand place, then 3 can be placed in any of the 3 places in 3 ways. Remaining two blanks can be filled with remaining eight digits in 8P2 ways. The number of numbers that have 7 is in thousand place is 3 x 8P2 = 168 Thousand place cannot be 0,7 and 3, it can be filled with remaining 7 digits in 7 ways. In remaining 3 blanks, 7 and 3 can be arranged in 3 ways. Fourth blank can be filled in 7 ways. The number of numbers that are formed where 7 and 3 is not in thousand place is 7x3x7 =147 . Hence total required numbers =168+147 = 315 .
CAT 2020 QA Slot 3 | Modern Math – Permutation & Combination CAT Question
How many integers in the set {100, 101, 102, …, 999} have at least one digit repeated?
EXPLANATION

CAT 2019 QA Slot 1 | Modern Math – Permutation & Combination CAT Question
With rectangular axes of coordinates, the number of paths from (1, 1) to (8, 10) via (4, 6), where each step from any point (x, y) is either to (x, y + 1) o to (x + 1, y), is
EXPLANATION
Explanation: To find the number of paths from (1, 1) to (8, 10) via (4, 6) using only vertical and horizontal steps, we can break down the problem into smaller subproblems. Step 1: Paths from (1, 1) to (4, 6) To reach (4, 6) from (1, 1), we need to take 3 horizontal (right) steps and 5 vertical (up) steps. The number of ways to do this can be calculated using combinations. We need to choose 3 out of 8 steps to be horizontal, so the number of ways is given by: C(3, 8) = 8!/[(8-3)!*3!] = 56 Step 2: Paths from (4, 6) to (8, 10) To reach (8, 10) from (4, 6), we need to take 4 horizontal (right) steps and 4 vertical (up) steps. The number of ways to do this can also be calculated using combinations: C(4, 8) = 8!/[(8-4)!*4!] = 70 Step 3: Paths via (4, 6) Now, we need to find the number of paths that go through (4, 6). Since the paths from (1, 1) to (4, 6) and from (4, 6) to (8, 10) are independent, we can multiply the number of ways in each step to get the total number of paths: Total paths = Paths from (1, 1) to (4, 6) * Paths from (4, 6) to (8, 10) Total paths = 56 * 70 = 3920 Therefore, the correct answer is 3920.
CAT 2018 QA Slot 1 | Modern Math – Permutation & Combination CAT Question
How many numbers with two or more digits can be formed with the digits 1, 2, 3, 4, 5, 6, 7, 8, 9, so that in every such number, each digit is used a most once and the digits appear in the ascending order?
EXPLANATION

CAT 2018 QA Slot 2 | Modern Math – Permutation & Combination CAT Question
In a tournament, there are 43 junior level and 51 senior level participants. Each pair of juniors play one match. Each pair of seniors play one match There is no junior versus senior match. The number of girl versus girl matches in junior level is 153, while the number of boy versus boy matches i senior level is 276. The number of matches a boy plays against a girl is
EXPLANATION

CAT 2017 QA Slot 1 | Modern Math – Permutation & Combination CAT Question
The number of solutions (x, y, z) to the equation x – y – z = 25, where x, y, and z are positive integers such that x ≤ 40, y ≤ 12, and z ≤ 12 is
(a) 101
(b)99
(C)87
(d) 105
EXPLANATION

CAT 2017 QA Slot 1 | Modern Math – Permutation & Combination CAT Question
Let AB, CD, EF, GH, and JK be five diameters of a circle with center at O. In how many ways can three points be chosen out of A, B, C, D, E, F, G, H, J, K and O so as to form a triangle?
EXPLANATION

CAT 2017 QA Slot 1 | Modern Math – Permutation & Combination CAT Question
In how many ways can 7 identical erasers be distributed among 4 kids in such a way that each kid gets at least one eraser but nobody gets more tha 3 erasers?
(a)16
(b)20
(c)14
(d)15
EXPLANATION

CAT 2017 QA Slot 2 | Modern Math – Permutation & Combination CAT Question
In how many ways can 8 identical pens be distributed among Amal, Bimal, and Kamal so that Amal gets at least 1 pen, Bimal gets at least 2 pens, an Kamal gets at least 3 pens?
EXPLANATION
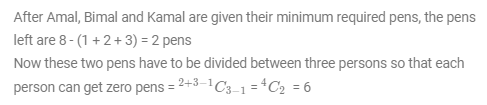
CAT 2017 QA Slot 2 | Modern Math – Permutation & Combination CAT Question
How many four digit numbers, which are divisible by 6, can be formed using the digits 0, 2, 3, 4, 6, such that no digit is used more than once and does not occur in the left-most position?
EXPLANATION

Directions for next 2 questions:
The figure below shows the plan of a town. The streets are at right angles to each other. A rectangular park (P) is situated inside the town with a diagonal road running through it. There is also a prohibited region (D) in the town.
CAT 2008 QA | Modern Math – Permutation & Combination CAT Question
Neelam rides her bicycle from her house at A to her office at B, taking the shortest path. Then the number of possible shortest paths that she ca choose is
a 60
b 75
c 45
d 90
e 72
EXPLANATION

CAT 2008 QA | Modern Math – Permutation & Combination CAT Question
Neelam rides her bicycle from her house at A to her club at C, via B taking the shortest path. Then the number of possible shortest paths that she ca choose is
(a) 1170
(b) 630
(c) 792
(d) 1200
(e) 936
EXPLANATION

CAT 2008 QA | Modern Math – Permutation & Combination CAT Question
How many integers, greater than 999 but not greater than 4000, can be formed with the digits 0, 1, 2, 3 and 4, if repetition of digits is allowed?
(a) 499
(b) 500
(c) 375
(d) 376
(e) 501
EXPLANATION
The smallest number in the series is 1000, a 4-digit number.
The largest number in the series is 4000, the only 4-digit number to start with 4.
The left most digit (thousands place) of each of the 4 digit numbers other than 4000 can take one of the 3 values 1 or 2 or 3.
The next 3 digits (hundreds, tens and units place) can take any of the 5 values 0 or 1 or 2 or 3 or 4.
Hence, there are 3 × 5 × 5 × 5 or 375 numbers from 1000 to 3999
Including 4000, there will be 376 such numbers.
CAT 2008 QA | Modern Math – Permutation & Combination CAT Question
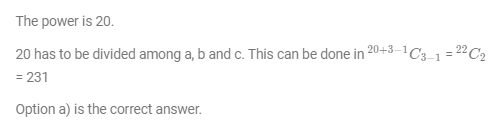
What is the number of distinct terms in the expansion of (a + b + c)20?
(a) 231
(b) 253
(c) 242
(d) 210
(e) 228
EXPLANATION
CAT 2007 QA | Modern Math – Permutation & Combination CAT Question
In a tournament, there are n teams T1 , T2 , Tn with n > 5. Each team consists of k players, k > 3. The following pairs of teams have one player i
common:
T1 & T2 , T2 & T3 ,……, Tn − 1 & Tn , and Tn & T1.
No other pair of teams has any player in common. How many players are participating in the tournament, considering all the n teams together?
A n(k – 1)
B k(n – 1)
C n(k – 2)
D k(k – 2)
(e) (n – 1)(k – 1)
Details
Let’s analyze the given information step by step to find the total number of players participating in the tournament. Number of Teams: – The given information states that there are n teams, denoted as T1, T2, …, Tn. – It is also mentioned that n is greater than 5. Number of Players per Team: – Each team consists of k players. – It is given that k is greater than 3. Common Players: – The given information states that the pairs of teams T1 and T2, T2 and T3, …, Tn-1 and Tn, and Tn and T1 have one player in common. – No other pair of teams has any player in common. Total Number of Players: To find the total number of players participating in the tournament, we need to consider all the teams together. – The first team T1 has k players. – The second team T2 has k players, with one player common with T1. – Similarly, the third team T3 also has k players, with one player common with T2. – This pattern continues until the last team Tn, which also has k players, with one player common with T1. – So, considering all the teams together, we can say that there are (n-1) common players, as each team has one player common with the next team. – Therefore, the total number of players participating in the tournament would be the sum of the players in each team, excluding the common players. – Total number of players = (k * n) – (n – 1) = kn – n + 1. Therefore, the correct answer is option ‘D’: n(k – 1).
CAT 2006 QA | Modern Math – Permutation & Combination CAT Question
There are 6 tasks and 6 persons. Task 1 cannot be assigned either to person 1 or to person 2; task 2 must be assigned to either person 3 or person 4 Every person is to be assigned one task. In how many ways can the assignment be done?
(a) 144
(b) 180
(c) 192
(d) 360
(e) 716
EXPLANATION
CAT 2005 QA | Modern Math – Permutation & Combination CAT Question
In a chess competition involving some boys and girls of a school, every student had to play exactly one game with every other student. It was foun that in 45 games both the players were girls, and in 190 games both were boys. The number of games in which one player was a boy and the othe was a girl is
(a) 200
(b) 216
(c) 235
(d) 256
EXPLANATION
In a chess competition that includes both boys and girls from a school, each student had to play exactly one game against every other student. We are asked to find the number of games in which one player was a boy and the other was a girl.
Let’s denote the number of boys as ‘B’ and the number of girls as ‘G’.
The total number of games played in the competition can be calculated using the combination formula: (B + G)C2 = (B + G) * (B + G – 1) / 2.
Given that 45 games were played between two girls, we can deduce that the number of games played between two boys is 190. Therefore, the number of games played between a boy and a girl is:
(B + G) * (B + G – 1) / 2 – 190 – 45.
Since each student played exactly one game with every other student, the total number of games played by a student is (B + G – 1). The total number of games played by all the students is (B + G) * (B + G – 1).
So, the number of games played between a boy and a girl can also be expressed as:
(B + G) * (B + G – 1) – 2 * 190 – 2 * 45.
We are given that this number is equal to the product of the number of boys and the number of girls, i.e., BG. Therefore, we have the equation:
B^2 + G^2 – B – G – 235 = BG.
Solving this equation, we find that BG is equal to 200, which means the number of games in which one player was a boy and the other was a girl is 200, matching option A.
CAT 2005 QA | Modern Math – Permutation & Combination CAT Question
Let S be the set of five digit numbers formed by the digits 1, 2, 3, 4 and 5, using each digit exactly once such that exactly two odd positions ar occupied by odd digits. What is the sum of the digits in the rightmost position of the numbers in S?
A 228
B 216
C 294
D 192
EXPLANATION
Certainly, here’s a rephrased summary of the explanation:
We are given three cases for forming numbers with specific patterns of odd (O) and even (E) digits:
Case 1: O _ O _ E
- There are 3 choices for the first digit (1, 3, 5).
- The third digit can be selected from the remaining odd digits (2 choices).
- The fifth digit can be any even digit (2 choices).
- The second and fourth digits are then chosen from the remaining digits (2 choices each).
- This results in 48 possible numbers in this case, with half ending in 2 and the other half in 4.
Case 2: O _ E _ O
- Similar to Case 1, there are 24 ways to create numbers in this case.
- 8 of them end with 1, 8 with 3, and 8 with 5.
Case 3: E _ O _ O
- Like Case 2, there are 24 possible numbers.
- 8 of them end with 1, 8 with 3, and 8 with 5.
For each case, the sum of the rightmost digits is calculated.
- Sum for Case 1 = 72.
- Sum for Case 2 = 72.
- Sum for Case 3 = 72.
The total sum of the rightmost digits for all cases combined is 216.
Therefore, the correct answer is option B.
CAT 2004 QA | Modern Math – Permutation & Combination CAT Question
N persons stand on the circumference of a circle at distinct points. Each possible pair of persons, not standing next to each other, sings a two-minut song one pair after the other. If the total time taken for singing is 28 minutes, what is N?
(a) 5
(b) 7
(c) 9
(d) None of the above
EXPLANATION
Certainly, here
To address this problem, let’s break it down step by step:
Step 1: Calculate the total number of pairs – We use the combination formula C(N, 2) to determine how many pairs can be formed from N distinct persons.
Step 2: Account for non-adjacent pairs – Since the problem specifies that adjacent pairs are not allowed, we need to subtract the number of adjacent pairs. There are N adjacent pairs because each person has two neighbors.
Step 3: Determine the total time – Each pair takes 2 minutes to sing, so we calculate the total time by multiplying (Total number of pairs – Number of adjacent pairs) by 2.
Step 4: Set up and solve the equation – We are given that the total time is 28 minutes. So, we create the equation: 28 = (C(N, 2) – N) * 2. After simplifying and solving, we find the value of N.
The final equation becomes: N^2 – 3N – 28 = 0, which is factored to (N – 7)(N + 4) = 0. Since the number of persons (N) cannot be negative, the correct answer is N = 7.
Hence, the answer is option B: 7.
CAT 2004 QA | Modern Math – Permutation & Combination CAT Question
In the adjoining figure, the lines represent one-way roads allowing travel only northwards or only westwards. Along how many distinct routes can a ca reach point B from point A?

A 15
B 56
C 120
D 336
EXPLANATION
Correct Option: B
Here , number of vertical steps ( v ) = 3
Number of horizontal steps ( h ) = 5
Then in this case total number of ways is given by h+vCh = h+vCv = 8C3 = 6 x 7 x ( 8/6 ) = 7 x 8 = 56.
Hence , 56 distinct routes can a car reach point B from point A .
CAT 2004 QA | Modern Math – Permutation & Combination CAT Question
A new flag is to be designed with six vertical stripes using some or all of the colours yellow, green, blue and red. Then, the number of ways this can b done such that no two adjacent stripes have the same colour is:
A 12 × 81
B 16 × 192
C 20 × 125
D 24 × 216
EXPLANATION
Solution
First strip can be colored by =4ways
2nd strip can be colored by =3ways
3rd strip can be colored by =3ways
4th strip can be colored by =3ways
5th strip can be colored by =3ways
6th strip can be colored by =3ways
Then total ways=4×3×3×3×3×3=12×34=12×81 Ans.
Hence, this is the answer.Option (A) is correct answer.
CAT 2004 QA | Modern Math – Permutation & Combination CAT Question
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Tarak is standing 2 steps to the left of a red mark and 3 steps to the right of a blue mark. He tosses a coin. If it comes up heads, he moves one step t the right; otherwise he moves one step to the left. He keeps doing this until he reaches one of the two marks, and then he stops. At which mark doe he stop?
He stops after 21 coin tosses.
He obtains three more tails than heads.
(a) 1
(b) 2
(c) 3
(d) 4
EXPLANATION
To determine at which mark Tarak stops, we need to consider both statements together:
Statement A: He stops after 21 coin tosses.
This statement alone does not provide enough information about the initial position of Tarak concerning the red and blue marks. It only tells us the number of coin tosses, but we need to know the starting position to decide which mark he reaches.
Statement B: No information is provided in Statement B.
Now, when we combine both statements, we know that Tarak stops after 21 coin tosses. However, without any information about the starting position concerning the red and blue marks, we still cannot determine at which mark he stops.
So, the correct answer is 4: The question cannot be answered based on the two statements.
CAT 2003 QA – Leaked | Modern Math – Permutation & Combination CAT Question
Twenty-seven persons attend a party. Which one of the following statements can never be true?
There is a person in the party who is acquainted with all the twenty-six others.
Each person in the party has a different number of acquaintances.
There is a person in the party who has an odd number of acquaintances.
In the party, there is no set of three mutual acquaintances.
CAT 2003 QA – Leaked | Modern Math – Permutation & Combination CAT Question
How many three digit positive integers, with digits x, y and z in the hundred’s, ten’s and unit’s place respectively, exist such that x < y, z < y and x ≠ 0?
A 245
B 285
C 240
D 320
Details
The condition specifies that the middle digit must be the largest of the three digits. Following this condition, the number of possible integers is determined for each value of y:
- For y = 1, there are no possible numbers as x cannot be zero.
- For y = 2, with x = 1 and z = 0 or 1, there are 2 possible numbers.
- For y = 3, with x = 1, 2 and z = 0, 1, 2, there are 2 * 3 = 6 possible numbers.
- This pattern continues for higher values of y, and for y = 9, there are 8 * 9 = 72 possible numbers.
To find the total number of three-digit positive integers that meet the condition, the possibilities for each y value are summed up:
(1 * 2) + (2 * 3) + (3 * 4) + (4 * 5) + (5 * 6) + (6 * 7) + (7 * 8) + (8 * 9) = 240.
Hence, the total number of three-digit positive integers that satisfy the specified condition is 240.
CAT 2003 QA – Leaked | Modern Math – Permutation & Combination CAT Question
There are 6 boxes numbered 1, 2,…, 6. Each box is to be filled up either with a red or a green ball in such a way that at least 1 box contains a green ba and the boxes containing green balls are consecutively numbered. The total number of ways in which this can be done is
(a) 5
(b) 21
(c) 33
(d) 60
EXPLANATION
(B) The number of ways in which 1 green ball can be put =6 . The number of ways in which two green balls can be put such that the boxes are consecutive
=5 (i.e.,(1,2),(2,3),(3,4),(4,5),(5,6))
CAT 2003 QA – Leaked | Modern Math – Permutation & Combination CAT Question
A graph may be defined as a set of points connected by lines called edges. Every edge connects a pair of points. Thus, a triangle is a graph with edges and 3 points. The degree of a point is the number of edges connected to it. For example, a triangle is a graph with three points of degree each. Consider a graph with 12 points. It is possible to reach any point from any other point through a sequence of edges. The number of edges, e, i the graph must satisfy the condition
A 11 ≤ e ≤ 66
B 10 ≤ e ≤ 66
C 11 ≤ e ≤ 65
D 0 ≤ e ≤ 11
Details
In a graph with 12 points, if it’s possible to reach any point from any other point through a sequence of edges, then it’s a connected graph. For a connected graph with ‘n’ points (vertices), it must have at least ‘n-1’ edges to ensure connectivity.
In this case, with 12 points, the graph must have at least 12 – 1 = 11 edges to satisfy the condition of being able to reach any point from any other point through a sequence of edges. Therefore, the number of edges, ‘e,’ in the graph must be at least 11
The correct answer is:
A) 11 ≤ e ≤ 66
In a graph with 12 points, it must have at least 11 edges to ensure connectivity, and it can have a maximum of 66 edges (in a complete graph with 12 vertices). So, the number of edges, ‘e,’ in the graph must satisfy the condition 11 ≤ e ≤ 66.
.
CAT 2003 QA – Retake | Modern Math – Permutation & Combination CAT Question
There are 12 towns grouped into four zones with three towns per zone. It is intended to connect the towns with telephone lines such that every tw towns are connected with three direct lines if they belong to the same zone, and with only one direct line otherwise. How many direct telephone line are required?
(a) 72
(b) 90
(c) 96
(d) 144
EXPLANATION
For towns within the same zone, there are 4 zones, each with 3 towns, resulting in a total of (4 zones) * (3 towns per zone) = 12 towns. Since each pair of towns in the same zone needs 3 direct lines, the total number of lines for towns within the same zone is 12 pairs * 3 lines per pair = 36 lines.
For towns in different zones, there are 12 towns in total. Since each town needs to connect to 9 other towns in different zones, and each connection requires one direct line, the total number of lines for towns in different zones is 12 towns * 9 lines per town = 108 lines.
Now, to find the total number of direct telephone lines required, add the lines needed for towns in the same zone and towns in different zones:
Total direct lines = Lines for towns in the same zone + Lines for towns in different zones
Total direct lines = 36 + 108
Total direct lines = 144
So, the correct answer is (d) 144.
CAT 2003 QA – Retake | Modern Math – Permutation & Combination CAT Question
An intelligence agency forms a code of two distinct digits selected from 0, 1, 2, … , 9 such that the first digit of the code is non-zero. The code handwritten on a slip, can however potentially create confusion, when read upside down – for example, the code 91 may appear as 16. How man codes are there for which no such confusion can arise?
(a) 80
(b) 78
(c) 72
(d) 69
EXPLANATION
To ensure that no confusion arises when reading the code upside down, we need to consider the following:
- The digits that remain the same when flipped upside down are 0, 1, and 8.
- The digits that look like other digits when flipped are 6 and 9, or vice versa.
Given these considerations, let’s count the possible codes:
- For the first digit (the non-zero digit), we have 9 choices (1 through 9).
- For the second digit, we can choose from the digits 0, 1, 8 (which don’t change when flipped), and we have 3 choices.
- For the third digit, we can choose from the digits 0, 1, 8 again, which gives us 3 choices.
So, there are a total of 9 (choices for the first digit) * 3 (choices for the second digit) * 3 (choices for the third digit) = 81 possible codes.
However, we need to subtract the cases where the second digit is the same as the first digit, as it can create confusion (for example, 11 looks the same upside down). There are 9 such cases (1 through 9 with the second digit the same as the first).
Therefore, the total number of codes for which no confusion can arise is 81 – 9 = 72.
CAT 2002 QA | Modern Math – Permutation & Combination CAT Question
n1, n2, n3 … n10 are 10 numbers such that n1 > 0 and the numbers are given in ascending order. How many triplets can be formed using these number such that in each triplet, the first number is less than the second number, and the second number is less than the third number?
A 120
B 27
C 36
D None of these
EXPLANATION
To find the number of triplets that can be formed using the 10 numbers {n1, n2, n3, …, n10} such that in each triplet, the first number is less than the second number, and the second number is less than the third number, we can analyze the possibilities.
Since the numbers are given in ascending order, we can form triplets by choosing any three numbers from the set {n1, n2, n3, …, n10}. The order in which we choose the numbers doesn’t matter because the numbers are distinct, and the arrangement within a triplet is not relevant.
To count the number of such triplets, we can use combinations. The number of ways to choose 3 numbers from 10 is given by the combination formula (C(n, k)):
C(10, 3) = 10! / (3!(10 – 3)!) = 10! / (3! * 7!) = (10 * 9 * 8) / (3 * 2 * 1) = 120.
So, there are 120 different triplets that can be formed. The correct answer is (A) 120.
CAT 2002 QA | Modern Math – Permutation & Combination CAT Question
How many numbers between 0 and one million can be formed using 0, 7 and 8?
A 486
B 1086
C 728
D None of these
EXPLANATION
To find out how many numbers between 0 and one million can be formed using the digits 0, 7, and 8, we need to consider the various possibilities for each digit’s place:
- Number of choices for the first digit: It can be 0, 7, or 8. So, there are 3 choices for the first digit.
- Number of choices for the second digit: It can be 0, 7, or 8. Again, there are 3 choices for the second digit.
- Number of choices for the third digit: It can be 0, 7, or 8. Once more, there are 3 choices for the third digit.
- Number of choices for the fourth digit: It can be 0, 7, or 8. As before, there are 3 choices for the fourth digit.
- Number of choices for the fifth digit: It can be 0, 7, or 8. There are 3 choices for the fifth digit.
- Number of choices for the sixth digit: It can be 0, 7, or 8. There are 3 choices for the sixth digit.
Now, to find the total number of numbers that can be formed, multiply the number of choices for each digit’s place together:
Total = 3 * 3 * 3 * 3 * 3 * 3 = 3^6 = 729.
However, this calculation includes the number “000000,” which is not between 0 and one million. Therefore, we need to subtract this one case from the total.
Total – 1 = 729 – 1 = 728.
So, there are 728 numbers between 0 and one million that can be formed using the digits 0, 7, and 8.
The correct answer is (C) 728.
CAT 2002 QA | Modern Math – Permutation & Combination CAT Question
In how many ways, we can choose a black and a white square on a chess board such that the two are not in the same row or column?
(a) 32
(b) 96
(c) 24
(d) None of these
EXPLANATION
We know a chess board has 32 white and 32 black squares, we need to select 1 white square out of these 32 white squares that is done in 32C1 which is 32 No, we have selected any one white square, there are eight black squares lying in the same column or row so out of 32−8=24 black squares We need to select one black square that is 24C1So, if both squares selected then our work is done Hence it is in 32×24=768 ways.
Answer the following question based on the information given below.
There are 11 alphabets A, H, I, M, O, T, U, V, W, X, Y. They are called symmetrical alphabets. The remaining alphabets are known as asymmetrical alphabets.
CAT 2002 QA | Modern Math – Permutation & Combination CAT Question
How many four-lettered passwords can be formed by using symmetrical letters only? (repetitions not allowed)
A 1086
B 255
C 7920
D None of these
EXPLANATION
In English alphabets 11 letters are there which are symmetric.So, total ways =11×10×9×8 =7920 Hence, the answer is 7920.
CAT 2002 QA | Modern Math – Permutation & Combination CAT Question
How many three-lettered words can be formed such that at least one symmetrical letter is there?
A 12870
B 18330
C 16420
D None of these
EXPLANATION
here are a total of 11 symmetric letters, and therefore, 15 asymmetric letters.
Method 1: Total number of words possible (no repetition):
26*25*24 = 650*24 = 15600
Total number of words possible with only asymmetric letters:
15*14*13 = 210*13 = 2730
Total number of words with at least one symmetric letter:
15600 – 2730 = 12870
Method 2 :
case1 : Total combination possible with 1 symmetrical and 2 asymmetrical :
The symmetrical number can be in any one of the digits. So, totally 3 possibilities.
Hence, the total combination = 11* 15 * 14 * 3 = 6930
case 2: Total combination possible with 2 symmetrical and 1 asymmetrical :
The asymmetrical number can be in any one of the digits. So, totally 3 possibilities.
Hence, the total combination = 11* 10 * 15 * 3 = 4950
case 3: Total combination possible with 3 symmetrical:
All the letters symmetrical Hence, the total combination = 11* 10*9 = 990
Hence, total possible combination= 6930 + 4950 + 990 = 12870.
Hence,(A)12870 is the Answer.
CAT 2001 QA | Modern Math – Permutation & Combination CAT Question
The figure below shows the network connecting cities A, B, C, D, E and F. The arrows indicate permissible direction of travel. What is the number o distinct paths from A to F?

(a) 9
(b) 10
(c) 11
(d) None of these
EXPLANATION
B) The maximum routes from A to F are listed below.
CAT 2001 QA | Modern Math – Permutation & Combination CAT Question
Let n be the number of different 5 digit numbers, divisible by 4 with the digits 1, 2, 3, 4, 5 and 6, no digit being repeated in the numbers. What is th value of n?
A 144
B 168
C 192
D None of these
EXPLANATION

CAT 2000 QA | Modern Math – Permutation & Combination CAT Question
One red flag, three white flags and two blue flags are arranged in a line such that,
no two adjacent flags are of the same colour.
the flags at the two ends of the line are of different colours. In how many different ways can the flags be arranged?
(a) 6
(b) 4
(c) 10
(d) 2
EXPLANATION

CAT 2000 QA | Modern Math – Permutation & Combination CAT Question
Sam has forgotten his friend’s seven-digit telephone number. He remembers the following: the first three digits are either 635 or 674, the number i odd, and the number nine appears once. If Sam were to use a trial and error process to reach his friend, what is the minimum number of trials he ha to make before he can be certain to succeed?
A 1000
B 2430
C 3402
D 3006
EXPLANATION

CAT 2000 QA | Modern Math – Permutation & Combination CAT Question
There are three cities A, B and C, each of these cities is connected with the other two cities by at least one direct road. If a traveller wants to go fro one city (origin) to another city (destination), she can do so either by traversing a road connecting the two cities directly, or by traversing two road the first connecting the origin to the third city and the second connecting the third city to the destination. In all there are 33 routes from A to (including those via C). Similarly there are 23 routes from B to C (including those via A). How many roads are there from A to C directly?
(a) 6
(b) 3
(c) 5
(d) 10
Details

CAT 2000 QA | Modern Math – Permutation & Combination CAT Question
ABCDEFGH is a regular octagon. A and E are opposite vertices of the octagon. A frog starts jumping from vertex to vertex, beginning from A. From an vertex of the octagon except E, it may jump to either of the two adjacent vertices. When it reaches E, the frog stops and stays there. Let an be the number of distinct paths of exactly n jumps ending in E. Then what is the value of a2n – 1?
Zero
Four
2n – 1
Cannot be determined
EXPLANATION

CAT 1999 QA | Modern Math – Permutation & Combination CAT Question
Ten points are marked on a straight-line and 11 points are marked on another straight-line. How many triangles can be constructed with vertices fro among the above points?
A 495
B 550
C 1045
D 2475
Details

CAT 1999 QA | Modern Math – Permutation & Combination CAT Question
For a scholarship, at the most n candidates out of 2n + 1 can be selected. If the number of different ways of selection of at least one candidate is 63 the maximum number of candidates that can be selected for the scholarship is
(a) 3
(b) 4
(c) 6
(d) 5
EXPLANATION
Max. number of candidates to be selected is n out of 2n+1 and the ans is n=3
Total no. of candidates is 2×3+1=7. Since at least 1 candidate is to be selected
1 can be selected in 7 ways
2 can be selected in 7×6/2!=21 ways
3 can be selected in 7×6×5/3!=35 ways
So 1, 2 or 3 can be sected in 7+21+35=63 ways as given in the question. So n=3 satisfies the conditions.
How many numbers can be formed from 1, 2, 3, 4, 5, without repetition, when the digit at the unit’s place must be greater than that in the ten’s place?
(a) 54
(b) 60
(c) 17
(d) 2 × 4!
EXPLANATION
These problems apply to numerous disciplines of mathematics. This question has to do with permutations and combinations. It is challenging to select the best option because of the way the options are presented. Candidates must be able to comprehend the appropriate approach to eliciting the desired response. Out of the five possible answers, there is only one that is correct.
Without repeating digits, the total number of numbers that may be created from the digits 1, 2, 3, and 5 is 5*4*3*2*!, which equals 5! = 120.
Now, the unit digit will be larger than the tenth digit in half of them and smaller in the other half.
Let’s take the example of the numbers 1, 2, and 3. 3*2*1=6 is the total number of integers without repeating digits.
Numerals whose unit digit is higher than the tenth digit
123, 213, 312
Numbers whose tenth digit is higher than the digit of the unit
321, 132, 231
Total Number of Cases = 120/2 = 60.
Hence,
Correct option: B









