- CAT 2021 QA Slot 1 | Geometry – Mensuration CAT Question
If the area of a regular hexagon is equal to the area of an equilateral triangle of side 12 cm, then the length in cm of each side of the hexagon is
(a) 4√6
(b) √6
(c) 6√6
(d) 2√6
EXPLANATION
The length of each side of hexagon is 2√6cm.
Step-by-step explanation:
The side of an equilateral triangle is 12 cm.
Let “a” be the side of the regular hexagon.
Now,
area of regular hexagon= area of an equilateral traingle..
=6*(√3/4)*a*a=(√3/4)*12*12
=a*a=12*12/6
=a*a=24
=a=2√6
the length of each side of hexagon is 2√6cm.
- CAT 2020 QA Slot 1 | Geometry – Mensuration CAT Question
On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is
(a) 3√π( 56 )
(b) 4√π(3 + 9 )
(c) 3√π(5 + 12 )
(d) 5√π(3 + 9 )
EXPLANATION
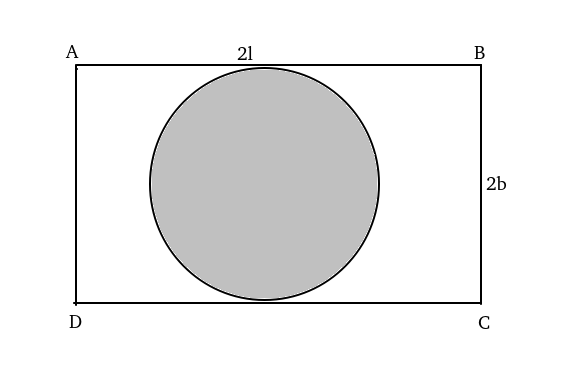

- CAT 2020 QA Slot 1 | Geometry – Mensuration CAT Question
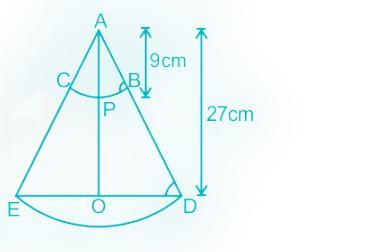
A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
(a) 256
(b) 232
(c) 264
(d) 243
EXPLANATION
Using the concept of Similar traingles,
△APB = △AOD
AP/AO = PB/OD
OD = 3 x PB
From the formula for the volume of cone,
Volume = 1/3 πr2
If the radius of the smaller cone is r cm, then the radius of the larger cone is 3r cm.
V (smaller cone) = (1/3) x π x (3r)2 x 9 = 3 πr2
V ( larger cone) = (1/3) x π x (3πr)2 x 27 = 81 πr2
Hence, the volume of the frustum CBDE = (81 – 27)πr2 = 78 πr2
225 = (78 – 3)πr2 = 75 πr2
πr2 = 225/75 = 3
r = √(3/π) cm
So, the radius of the larger cone (original)
3r = 3 x √(3/π) cm
The volume of the original cone = (1/3) x π x [ 3 x √(3/π)]2 x 27 = 243 cm3
- CAT 2019 QA Slot 1 | Geometry – Mensuration CAT Question
If the rectangular faces of a brick have their diagonals in the ratio 3 : 2√3 : √15, then the ratio of the length of the shortest edge of the brick to that o its longest edge is?
(a) √3 : 2
(b) 2 : √5
(c) 1 : √3
(d) √2 : √3
EXPLANATION

- CAT 2019 QA Slot 2 | Geometry – Mensuration CAT Question
The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertica height of the pyramid, in cm, is
(a) 10√2
(b) 8√3
(c) 12
(d) 5√5
EXPLANATION

From the diagram, it is clear that AB is the slant height of the equilateral triangle and is also the slant height of the pyramid.
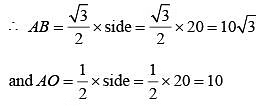
On applying Pythagoras theorem in triangle AOB,
OB2 = AB2 – OA2 = (10√3 )2 − 102 = 200
∴ Height of the pyramid OB = 10√2 cm
- CAT 2019 QA Slot 2 | Geometry – Mensuration CAT Question
A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each typ of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, the the total surface area of all these cylinders, in sq cm, is
(a) 1044(4 + π)
(b) 8464π
(c) 928π
(d) 1026(1 + π)
EXPLANATION

- CAT 2018 QA Slot 1 | Geometry – Mensuration CAT Question
A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the bas and 9 ft from the base. With π = 22/7, the volume, in cubic ft, of the remaining part of the cone is
EXPLANATION
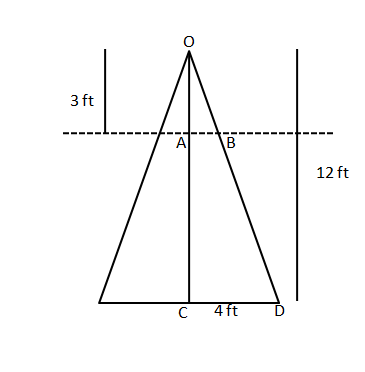
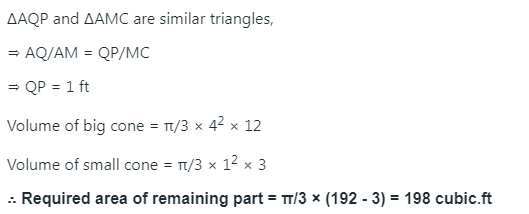
- CAT 2018 QA Slot 2 | Geometry – Mensuration CAT Question
From a rectangle ABCD of area 768 sqcm, a semicircular part with diameter AB and area 72π sqcm is removed. The perimeter of the leftover portion, i cm, is:
(a) 88 + 12π
(b) 82 + 24π
(c) 80 + 16π
(d) 86 + 8π
EXPLANATION
Area of the semicircle with AB as a diameter = 1/2 * π *(AB2/ 4)
=>1/2 * π *(AB2/ 4) = 72 * π
=> AB = 24cm
Given that area of the rectangle ABCD = 768 sq.cm
=>AB*BC = 768 =>BC = 32 cm
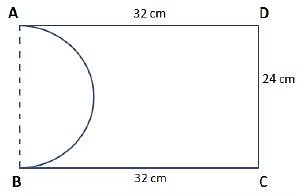
We can see that the perimeter of the remaining shape = AD + DC + BC + Arc(AB)
=> 32+24+32+π * 24/2
=> 88 + 12π
- CAT 2017 QA Slot 1 | Geometry – Mensuration CAT Question
A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8 : 27 : 27. The percentage by which the sum of th surface areas of these five cubes exceeds the surface area of the original cube is nearest to:
(a) 10
(b) 50
(c) 60
(d) 20
EXPLANATION
The correct option is B
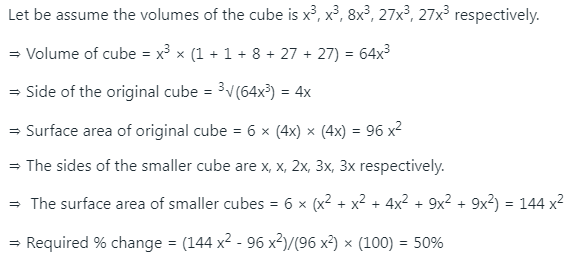
- CAT 2017 QA Slot 1 | Geometry – Mensuration CAT Question
A ball of diameter 4 cm is kept on top of a hollow cylinder standing vertically. The height of the cylinder is 3 cm, while its volume is 9π cm3. Then th vertical distance, in cm, of the topmost point of the ball from the base of the cylinder is:
EXPLANATION
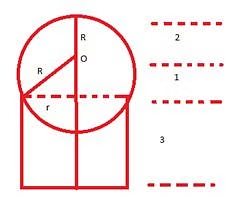
The height of the cylinder (h) = 3
The volume = 9π
πr2h = 9π ⇒ r = √3
The radius of the ball (R) = 2
The height of O, the centre of the ball, above the line representing the top of the cylinder is say a. (a = 1)
∴ The height of the topmost point of the ball from the base of the cylinder is h + a +R = 3 + 1 + 2 = 6
Answer: 6
- CAT 2017 QA Slot 2 | Geometry – Mensuration CAT Question
The base of a vertical pillar with uniform cross section is a trapezium whose parallel sides are of lengths 10 cm and 20 cm while the other two sides ar equal in length. The perpendicular distance between the parallel sides of the trapezium is 12 cm. If the height of the pillar is 20 cm, then the total area in sq cm, of all six surfaces of the pillar is
(a) 1300
(b) 1340
(c) 1480
(d) 1520
EXPLANATION
The correct option is C
1480
The diagram given below represents the cross-section of the pillar.
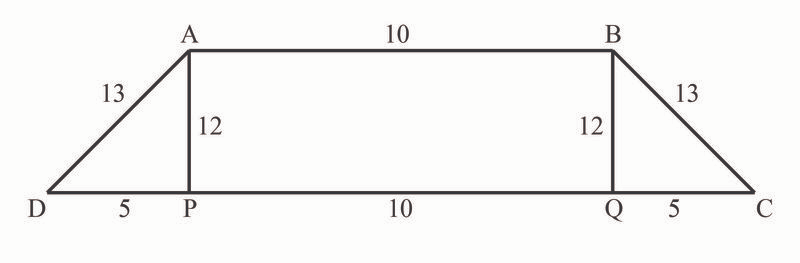
Total surface area of all the six surfaces = Area of 4 walls + Area of top and bottom
⇒(Perimeter of the trapezium x Height of the pillar) + 2 x Area of the trapezium⇒(10 + 13 + 13 + 20) x 20 + 2 x 12 x (10 + 20) x 12 ⇒1120 + 360 ⇒1480
- CAT 2017 QA Slot 2 | Geometry – Mensuration CAT Question
If three sides of a rectangular park have a total length 400 ft, then the area of the park is maximum when the length (in ft) of its longer side is
- CAT 2008 QA | Geometry – Mensuration CAT Question
Consider a right circular cone of base radius 4 cm and height 10 cm. A cylinder is to be placed inside the cone with one of the flat surface resting o the base of the cone. Find the largest possible total surface area (in sq. cm) of the cylinder.
(A)100π 3
(B)80π 3
(C)120π 7
(D)130π 9
(E)110π 7
EXPLANATION
As shown in the figure, ABC is the cross section of a cone of height 14 cm and radius of base 7 cm. PQRS is the cross section of a cylinder which needs to be fitted inside the cone such that one of the flat faces of the cylinder coincides with the base of the cone.
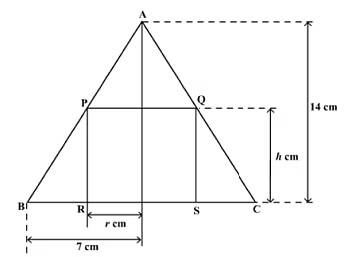
ΔAPQ and ΔABC are similar triangles.
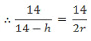
∴ h = 14 – 2r . . . (1)
Volume of the cylinder = V = πr2h
∴ V = πr2(14 – 2r)
∴ V = 14πr2 – 2πr3
Differentiating ‘V with respect to ‘r’,
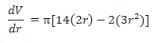
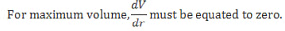
∴ 14(2r) – 2 (3r2) = 0
Solving the above equation we get r = 0 or 14/3.
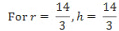
Maximum volume of the cylinder
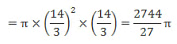
Hence, option 1.
- CAT 2007 QA | Geometry – Mensuration CAT Question
Each question is followed by two statements A and B. Answer each question using the following instructions.
Mark (1) if the question can be answered by using statement A alone but not by using statement B alone. Mark (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark (3) if the question can be answered by using both the statements together but not by using either of the statements alone.
Mark (4) if the question cannot be answered on the basis of the two statements.
ABC Corporation is required to maintain at least 400 Kilolitres of water at all times in its factory, in order to meet safety and regulatory requirement ABC is considering the suitability of a spherical tank with uniform wall thickness for the purpose. The outer diameter of the tank is 10 meters. Is th tank capacity adequate to meet ABC’s requirements?
A. The inner diameter of the tank is at least 8 meters.
B. The tank weighs 30,000 kg when empty, and is made of a material with density of 3 gm/cc.
(a) 1
(b) 2
(c) 3
(d) 4
(e) 5
Explanation
(P/m)< 1 is possible when p < m . Using statement A alone: ∴ p – m > 0 ∴ p > m ∴ p/m > 1 Thus, p/m is not less than one. Thus, the question can be answered using statement A alone. Using statement B alone: p < 8 and m – 8 > 0 ∴ m > 8 ∴ p < m ∴ p/m < 1 Thus, the question can be answered using statement B alone. Thus, the question can be answered using either statement alone. Hence option C is correct answer
- CAT 2006 QA | Geometry – Mensuration CAT Question
The length, breadth and height of a room are in the ratio 3 : 2 : 1. If the breadth and height are halved while the length is doubled, then the total are of the four walls of the room will
(a) remain the same.
(b) decrease by 13.64%.
(c) decrease by 15%.
(d) decrease by 18.75%.
(e) decrease by 30%.
Details
Explanation:
Let the length, breadth, and height of the cuboid as 3x, 2x, and x respectively.
Then, the area of four walls is given by 2(bh + lh) = 2h(l + b) = 2(x)(3x + 2x) = 2(x)(5x) = 10x2 sq.m
Given that,
- length is doubled: (3x) × 2 = 6x
- breadth is halved: 2x / 2 = x
- height is halved: x / 2 = x/2
Now, the new area of four walls
\text { Area }_{\text {new }} = 2(x/2)(6x + x) = 2 × (x/2) × (7x) = 7x2
\text { Area }_{\text {original }} = 10x2
The percentage increase = \left(\text { Are } a_{\text {new }} \text { – Area }_{\text {original }}\right) / \text { Area }_{\text {original }}
The percentage difference in the area of four walls = [ (7x2 – 10x2) / 10x2 ] × 100 = [ – 3x2 / 10x2 ] × 100 = [ -3/10 ] × 100 = – 30 %
The percentage difference in the area of four walls is – 30% (Negative sign shows decrease in area)
Thus, if the breadth and height are halved while the length is doubled, then the total area of the four walls of the room will decrease by 30%.
Answer the next 2 questions based on the information given below:
A punching machine is used to punch a circular hole of diameter two units from a square sheet of aluminium of width 2 units, as shown below. The hole is punched such that the circular hole touches one corner P of the square sheet and the diameter of the hole originating at P is in line Report
with a diagonal of the square.

- CAT 2006 QA | Geometry – Mensuration CAT Question
The proportion of the sheet area that remains after punching is:
(a) π+2/8
(b) 6−π/8
(c) 4−π/4
(d) π−2/4
(e) 14−3π/6
Details


- CAT 2006 QA | Geometry – Mensuration CAT Question
Find the area of the part of the circle (round punch) falling outside the square sheet.
(a) π/4
(b) π−1/2
(c) π−1/4
(d) π−2/2
(e) π−2/4
Details
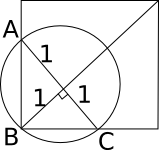
The area of triangle ABC is 1/2 * 2 2* 2 2= 1 Area of semi-circle ABC = � / 2 π/2 So, area of circle outside the square = � / 2 π/2 – 1 = ( � π -2)/2…
- CAT 2005 QA | Geometry – Mensuration CAT Question
A jogging park has two identical circular tracks touching each other, and a rectangular track enclosing the two circles. The edges of the rectangles ar tangential to the circles. Two friends, A and B, start jogging simultaneously from the point where one of the circular tracks touches the smaller side o the rectangular track. A jogs along the rectangular track, while B jogs along the two circular tracks in a figure of eight. Approximately, how much faste than A does B have to run, so that they take the same time to return to their starting point?
(a) 3.88%
(b) 4.22%
(c) 4.44%
(d) 4.72%
Details

Let the radius of 2 circles be r . Speed of A would be 12r/t and Speed of B would be 4*Pi*r/t . To find percentage faster B have to run than A we have : (4*Pi – 12)*100/ (4*Pi) = 4.46% approx. Hence, …
- CAT 2005 QA | Geometry – Mensuration CAT Question
Rectangular tiles each of size 70 cm by 30 cm must be laid horizontally on a rectangular floor of size 110 cm by 130 cm, such that the tiles do no overlap. A tile can be placed in any orientation so long as its edges are parallel to the edges of the floor. No tile should overshoot any edge of th floor. The maximum number of tiles that can be accommodated on the floor is
(a) 4
(b) 5
(c) 6
(d) 7
Details

As seen from the fig. If following configuration is used max 6 number of tiles that can be accommodated on the floor. …
- CAT 2005 QA | Geometry – Mensuration CAT Question
A rectangular floor is fully covered with square tiles of identical size. The tiles on the edges are white and the tiles in the interior are red. The number o white tiles is the same as the number of red tiles. A possible value of the number of tiles along one edge of the floor is
(a) 10
(b) 12
(c) 14
(d) 16
Details
Let the rectangle has x and y tiles along its length and breadth respectively. The number of white tiles W = 2x + 2(y – 2) = 2 (x + y – 2) And the number of red tiles = R = xy – 2 (x + y – 2) Given that the number of white tiles is the same as the number of red tiles ⇒ 2 (x + y – 2) = xy – 2 (x + y – 2) ⇒ 4 (x + y – 2) = xy ⇒ xy – 4x – 4y = –8 ⇒ (x – 4) (y – 4) = 8 = 8 �1 or 4 � 2 ⇒ m – 4 = 8 or 4 ⇒m = 12 or 8 Therefore, the number of tiles along one edge of the floor can be 12 Hence Option D is correct
- CAT 2004 QA | Geometry – Mensuration CAT Question
A rectangular sheet of paper, when halved by folding it at the mid-point of its longer side, results in a rectangle, whose longer and shorter sides are i the same proportion as the longer and shorter sides of the original rectangle. If the shorter side of the original rectangle is 2, what is the area of th smaller rectangle?
(a) 4√2
(b) 2√2
(c) √2
(d) None of the above
Details
Let the longer side of the original rectangle be x. Therefore, breadth of the modified rectangle = x/2. => x:2 = 2:(x/2) => � 2 x 2 = 8 Area of smaller rectangle = (x/2)*2 = x = 2 2 2 2…
- CAT 2004 QA | Geometry – Mensuration CAT Question
If the lengths of diagonals DF, AG and CE of the cube shown in the adjoining figure are equal to the three sides of a triangle, then the radius of the circle circumscribing that triangle will be .

(a) equal to the side of the cube
(b) √3 times the side of the cube
(c)1 times the side of the cube b√3
(d) impossible to find from the given information
Details
DF,AG and CE are body diagonals of cube Let the side of cube be a.Therefore, body diagonal is a √3Circum radius for equilateral triangle side√3Therefore, a√3√3=aThe answer is well described in the figure itself

- CAT 2003 QA – Leaked | Geometry – Mensuration CAT Question
Let A and B be two solid spheres such that the surface area of B is 300% higher than the surface area of A. The volume of A is found to be k% lowe than the volume of B. The value of k must be
(a) 85.5
(b) 92.5
(c) 90.5
(d) 87.5
Details
Let ra,rb be radius of A & B respectively
Given S.A of B is 300% greater then S.A of A ⇒4πr2b=4×4πr2a⇒rb=2raVolume of A(Va)=43πr3aVolume of B(Vb)=43π(rb)3=43π(2ra)3=8×43πr3aVb=8Va∴
Volume of A is 87.5% lower than B
- CAT 2003 QA – Leaked | Geometry – Mensuration CAT Question
There are 8436 steel balls, each with a radius of 1 centimeter, stacked in a pile, with 1 ball on top, 3 balls in the second layer, 6 in the third layer, 10 i the fourth, and so on. The number of horizontal layers in the pile is
(a) 34
(b) 38
(c) 36
(d) 32
Details
Let Sn denote the number of balls in row n.
Therefore, S2−S1=2
S3−S2=3S4−S3=4………Sn=Sn−1=n
Adding all the equations we get = Sn−S1=2+3+4+….+n.
Since S1=1,Sn=1+2+3+…+n=n(n+1)2.
Therefore total number of balls -sum of balls in all the row
=∑n(n+1)2=12(∑n2+∑n)=n(n+1)(2n+1)12+n(n+1)4
Given that total number of balls -8436→n(n+1)(2n+1)12+n(n+1)4=8436→n=36.
Hence, there are 36 layers in the pile.
Answer the following question based on the information given below.
Consider a cylinder of height h cm s and radius r = 2/π cm s as shown in the figure (not drawn to scale). A string of a certain length, when wound on its cylindrical surface, starting at point A and ending at point B, gives a maximum of n turns (in other words, the string’s length is the minimum length required to wind n turns.)
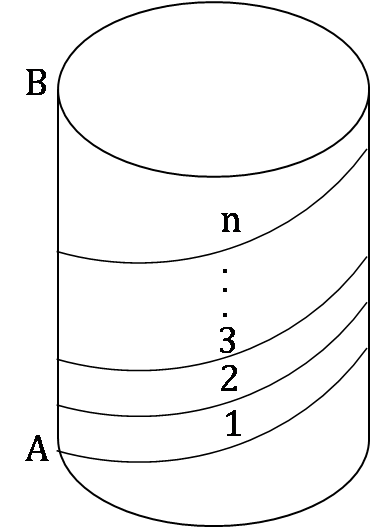
- CAT 2003 QA – Retake | Geometry – Mensuration CAT Question
What is the vertical spacing in cms between two consecutive turns?
(a) h/n
(b) h/√n
(c) h/n²
(d) Cannot be determined with given information
- CAT 2003 QA – Retake | Geometry – Mensuration CAT Question
The same string, when wound on the exterior four walls of a cube of side n cms, starting at point C and ending at point D, can give exactly one tur (see figure, not drawn to scale).
The length of the string, in cms, is
(a) √2n
(b) √17n
(c) n
(d) √13n
Details
- CAT 2003 QA – Retake | Geometry – Mensuration CAT Question
In the setup of the previous two questions, how is h related to n?
(a) h = √2n
(b) h = √17n
(c) h = n
(d) h = √13n
- CAT 2003 QA – Retake | Geometry – Mensuration CAT Question
Consider two different cloth-cutting processes. In the first one, n circular cloth pieces are cut from a square cloth piece of side a in the following step the original square of side a is divided into n smaller squares, not necessarily of the same size; then a circle of maximum possible area is cut from eac of the smaller squares. In the second process, only one circle of maximum possible area is cut from the square of side a and the process ends there The cloth pieces remaining after cutting the circles are scrapped in both the processes. The ratio of the total area of scrap cloth generated in th former to that in the latter is:
(a) 1 : 1
(b) √2 : 1
(c) n(4−π) 4n−π
(d) 4n−π n(4−π)
Details
In this question, we have to find the ratio of the total scrap generated by both the processes. We will consider a square of side x and then we will find the area of that square, that is,
Area of square = side
×× side
Area of square
=(x)2=(�)2
Now, we will cut the largest circle possible from the square of side x. So, the radius of the circle will be
(x2)(�2). Therefore, the area of the circle will be
Area of the circle =
πr2��2
Area of the circle =
π(x2)2�(�2)2
Area of the circle
=πx24=��24
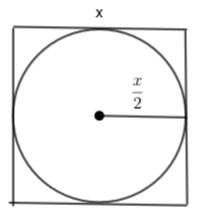
Now we will calculate the area of the scrap generated by cutting the piece of the circle from the square by using the formula.
Area of scrap = Area of the square – Area of the circle
Area of scrap
=x2−πx24=�2−��24
Area of scrap
=x2(1−π4)=�2(1−�4)
Now, we will divide the whole equation by
x2�2. So, we get,
Area of scrapx2=x2x2(1−π4)Area of scrap�2=�2�2(1−�4)
Area of scrapx2=(1−π4)Area of scrap�2=(1−�4)
where
x2�2 is the area of the square. So, we can write it as,
Area of scrapArea of the square=1−π4Area of scrapArea of the square=1−�4
From this, we can see that the ratio of the area of scrap to the ratio of the area of the square is always constant whether we cut the circle from a smaller square or larger square that means the scrapped area is always a fixed percentage of the square.
In this question, we have taken both squares of equal size. So, the ratio of the scrapped area will also be equal. Therefore we can say that the ratio of the scrap area in both the processes is equal, that means, in the ratio of 1:1.
Hence, option (a) is the right answer.
- CAT 2002 QA | Geometry – Mensuration CAT Question
In order to cover less distance, a boy – rather than going along the longer and the shorter lengths of the rectangular path, goes by the diagonal. Th boy finds that he saved a distance equal to half the longer side. The ratio of the breadth and length is
(a) 1/2
(b) 2/3
(c) 3/4
(d) 7/15
Details
Let A and B be the length and breadth respectively.
Diagonal of a rectangle (say C)(By Pythagoras theorem):::: C2=A2+B2–let this be (I)
Given,
C+0.5A=A + B
C=0.5A+B-let this be (II)
Puttin II in I
0.25A2+B2+AB=A2+B2
0.25A2+AB=A2
AB=A2-0.25A2
AB=0.75A2
AB/A2=0.75
B/A=3/4
THERFORE THE RATIO IS 3:4
- CAT 2002 QA | Geometry – Mensuration CAT Question
Neeraj has a rectangular field of size 20 × 40 sq.m. He has to mow the field with a mowing machine of width 1 m. If he mows the field from th extremes to the centre, then the number of rounds taken by him to mow half of the field will be
(a) 3.5
(b) 3.8
(c) 3
(d) 4
Details

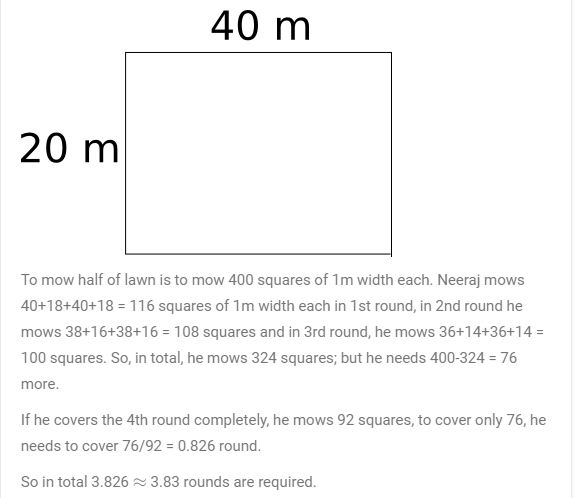
- CAT 2002 QA | Geometry – Mensuration CAT Question
On the corners of a square field of side 14 metres, 4 horses are tethered in such a way the adjacent horses just reach each other. There is a circula pond of area 20 sq.m. in the centre of the square. What is the area left ungrazed?
(a) 154 sq. m
(b) 22 sq. m
(c) 120 sq. m
(d) None of these
Details
Four horses are tethered at four corners of a square plot of side 14 metres (m) so that the adjacent horses can just reach one another. There is a small circular pond of area 20 m2 at the centre. The area left ungrazed is?
22.062… m²
Answer the following question based on the information given below.
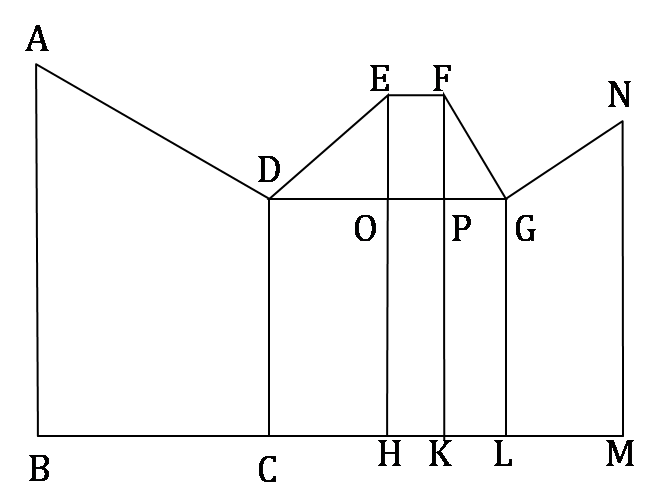
In the diagram below, ∠ABC = 90° = ∠DCH = ∠DOE = ∠EHK = ∠FKL = ∠GLM = ∠LMN, AB = BC = 2CH = 2CD = EH = FK = 2HK = 4KL
= 2LM = MN
- CAT 2002 QA | Geometry – Mensuration CAT Question
The magnitude of ∠FGO =
(a) 30°
(b) 45°
(c) 60°
(d) None of these
- CAT 2002 QA | Geometry – Mensuration CAT Question
The ratio of the areas of the two quadrangles ABCD and DEFG is
(a) 1 : 2
(b) 2 : 1
(c) 12 : 7
(d) None of these
- CAT 2002 QA | Geometry – Mensuration CAT Question
The ratio of the areas of the two quadrangles ABCD and DEFG is
(a) 1 : 2
(b) 2 : 1
(c) 12 : 7
(d) None of these
- CAT 2001 QA | Geometry – Mensuration CAT Question
A square, whose side is 2 meters, has its corners cut away so as to form an octagon with all sides equal. Then the length of each side of the octagon, i meters is
| A √2 √2+1 |
| B 2 √2+1 |
| C 2 √2−1 |
| D √2 √2−1 |
Details
Let ABCd is a square and AB = BC = CD= DA = 2 m Again, we form a rectangular octagon by cutting all four corners. Let EF = FG = GH = HI = IJ = JK = KL = LE = x Now, by symmetry, we get AE = Al = BG = BF = Ch = CI = DJ = Dk = a In triangle ALE, apply Pythagorus theorem, AL2= AE2+ LE2 => x2= a2+ a2 => x2= 2a2 => x = a√2 => a = x/√2 ………………..1 Again, AB = AE + EF + FB. => 2 = a + x + a => 2 = 2a + x => 2 = 2x/√2 + x => √2x + x = 2 => (√2 + 1)x = 2 => x = 2/(√2 + 1) So, the side of an octagon is 2/(√2 + 1) m
- CAT 2001 QA | Geometry – Mensuration CAT Question
Two sides of a plot measure 32 metres and 24 metres and the angle between them is a perfect right angle. The other two sides measure 25 metre each and the other three are not right angles.

What is the area of the plot?
(a) 768
(b) 534
(c) 696.5
(d) 684
Details
In right angle Δ ADC, AC2=AD2+DC2 ….By Pythagoras theorem⇒AC=√242+322−√576+1024=√1600 =40mFor ΔABC, s=25+25+402=45m∴ Area of the plot = Area of ΔADC+ Area of ΔABC=12×24×32+ +√45(45−25)(45−25)(45−40)=384+√45×20×20×5=384+300=684m2
- CAT 2001 QA | Geometry – Mensuration CAT Question
A rectangular pool 20 metres wide and 60 metres long is surrounded by a walkway of uniform width. If the total area of the walkway is 516 squar metres, how wide, in metres, is the walkway?
(a) 43
(b) 4.3
(c) 3
(d) 3.5
Details
We know the area of a rectangle== length××width or breath
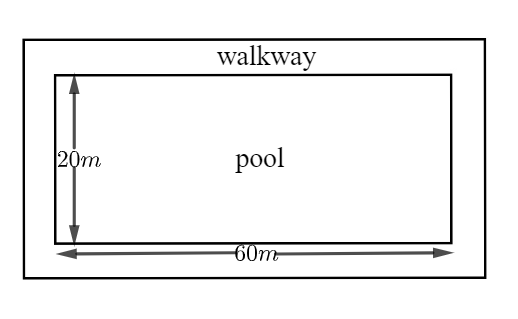
Given, the width of the pool=20m=20�
The length of the pool=60m=60�
So, the area of the pool=20×60=1200m2=20×60=1200�2
Now for the area of the rectangle
Let the width of the walkway be ‘x’ meters.
So the length of the rectangle consisting the pool and the walkway=60+x+x=60+2x=60+�+�=60+2�
And the width of the rectangle consisting the pool and the walkway=20+x+x=20+2x=20+�+�=20+2�
Hence, the area of the rectangle consisting the pool and the walkway=(60+2x)(20+2x)=(60+2�)(20+2�)
But as we know the area of the rectangle consisting the pool and the walkway== the area of the pool++the area of the walkway
And since the area of the walkway is given as 516m2516�2, hence it can be written as
(60+2x)(20+2x)=1200+516⇒1200+120x+40x+4×2=1716⇒4×2+160x+1200−1716=0⇒4×2+160x−516=0⇒4(x2+40x−129)=0⇒x2+40x−129=0⇒x=−40±402−4⋅1⋅(−129)−−−−−−−−−−−−−−−√2⋅1⇒x=−40±1600+516−−−−−−−−−√2⇒x=−40±2116−−−−√2⇒x=−40±462(60+2�)(20+2�)=1200+516⇒1200+120�+40�+4�2=1716⇒4�2+160�+1200−1716=0⇒4�2+160�−516=0⇒4(�2+40�−129)=0⇒�2+40�−129=0⇒�=−40±402−4⋅1⋅(−129)2⋅1⇒�=−40±1600+5162⇒�=−40±21162⇒�=−40±462
Either
x=−40+462⇒x=62⇒x=3�=−40+462⇒�=62⇒�=3
Or
x=−40−462⇒x=−862�=−40−462⇒�=−862
⇒x=−43⇒�=−43 (Not possible as ‘x’ is a width)
So, we can conclude that the walkway is 3 meters wide.
- CAT 2000 QA | Geometry – Mensuration CAT Question
Two full tanks, one shaped like a cylinder and the other like a cone, contain jet fuel. The cylindrical tank holds 500 litres more than the conical tank After 200 litres of fuel has been pumped out from each tank the cylindrical tank contains twice the amount of fuel in the conical tank. How many litre of fuel did the cylindrical tank have when it was full?
(a) 700
(b) 1000
(c) 1100
(d) 1200
Details
Let the current capacity of conical flask be C. So, cylinder = C+500. After pumping out 200 liters, C+300 = 2(C-200) => C = 700 So, full capacity of cylinder = 700+500 = 1200.
- CAT 2000 QA | Geometry – Mensuration CAT Question
A farmer has decided to build a wire fence along one straight side of his property. For this, he planned to place several fence-posts at six metr intervals, with posts fixed at both ends of the side. After he bought the posts and wire, he found that the number of posts he had bought was five les than required. However, he discovered that the number of posts he had bought would be just sufficient if he spaced them eight metres apart. What i the length of the side of his property and how many posts did he buy?
(a) 100 metres, 15
(b) 100 metres, 16
(c) 120 metres, 15
(d) 120 metres, 16
Details
The correct option is D 120 metres, 16
Let the length of the field be X m and let the number of fences he get be Y. Then as per the plan if the farmer tries to arrange them at a distance of 6m each, then there shall be 5 short. Also if he tries to place them 8m apart, then the number of fences required shall be perfectly matching the number available. Hence the equations shall look like: (X6)+1=Y+5;X8+1= Y. Solving Y = 16, also the value of X = 120m.
- CAT 1999 QA | Geometry – Mensuration CAT Question
There is a square field of side 500 m long each. It has a compound wall along its perimeter. At onec of its corners, a triangular area of the field is to b cordoned off by erecting a straight-line fence. The compound wall and the fence will form its borders. If the length of the fence is 100 m, what i the maximum area that can be cordoned off?
(a) 2,500 sq.m
(b) 10,000 sq.m
(c) 5,000 sq.m
(d) 20,000 sq.m
Details
The Length of the fence(100 m) would be the hypotenuse of the right triangular area which is cordoned.You should also realize that this triangular area would be an isosceles triangle.
Thus,by pythagoras theorem the legs of the right angled isosceles triangle would be :
1002 =2�2
�2=5000
�=502
Area of the triangles would be given by = 502 *502=2500 sq m
Hence,Option (A)2500 sq m is the correct choice
- CAT 1999 QA | Geometry – Mensuration CAT Question
Directions: Each question is followed by two statements I and II. Mark:
- if the question can be answered by any one of the statements alone, but cannot be answered by using the other statement alone.
- if the question can be answered by using either statement alone.
- if the question can be answered by using both the statements together, but cannot be answered by using either statement alone.
- if the question cannot be answered even by using both the statements together.
A small storage tank is spherical in shape. What is the storage volume of the tank?
I. The wall thickness of the tank is 1 cm.
II. When an empty spherical tank is immersed in a large tank filled with water, 20 l of water overflow from the large tank.
(a) 1
(b) 2
(c) 3
(d) 4
Details
The correct option is C C
From 1, we know that A is last, C is second last. So 1st rank can be occupied by B or D. So 1 alone cannot answer the question.From 2, we know that B is not among top 2 so B can be 3rd or 4th. Still we have no clue about who has the first rank. So statement 2 alone can’t give the answer. But when we combine both, we know that D is rank 1 because B is not in top 2. So the correct option is (c).
Direction: Answer the questions based on the following information.
A cow is tethered at point A by a rope. Neither the rope nor the cow is allowed to enter ΔABC.
∠BAC = 30°
I(AB) = I(AC) = 10 m
- CAT 1998 QA | Geometry – Mensuration CAT Question
What is the area that can be grazed by the cow if the length of the rope is 8 m?
(a) 134π 1 sq.m
(b) 121π sq.m
(c) 132π sq.m
(d)176π 3sq.m
Details
(d) 176 3 π 176 3 � sq. cm Given : AB = AC = 10 m, BC = 6 m and ∠A = 30º. The area that the cow can graze is the area of the circle with centre A and radius 8 m. But the cow is not allowed to enter the sector ADE formed inside DABC with ∠A = 30° and AD = AE = 8 cm. ∴ Area grazed = Area of circle – Area of sector ADE = πr2 – πr2 . 30 ° 360 ° 30 ° 360 ° = πr2 ( 1 − 30 ° 360 ° ) ( 1 − 30 ° 360 ° ) = π x 64 x 11 12 11 12 = 176 3 π 176 3 � sq. cmRead more on Sarthaks.com – https://www.sarthaks.com/1011897/cow-tethered-corner-rope-neither-the-cow-nor-the-rope-allowed-enter-abc-a-30-ab-ac-10-and-bc
- CAT 1998 QA | Geometry – Mensuration CAT Question
What is the area that can be grazed by the cow if the length of the rope is 12 m?
(a) 133π 1 sq.m
(b) 121π sq.m
(c) 132π sq.m
(d)176π 3sq.m
Details
Total Area covered by the cow =πr2 =(12)2π =144πm2Approximate area ,Option”D” is correct option, we get.Hence, this is the required answer.
- CAT 1996 QA | Geometry – Mensuration CAT Question
From a circular sheet of paper with a radius 20 cm, four circles of radius 5 cm each are cut out. What is the ratio of the uncut to the cut portion?
(a) 1 : 3
(b) 4 : 1
(c) 3 : 1
(d) 4 : 3
Details
Area of four small circles = 4 × π × 25 cm2 = 100π cm2 Area of the big circle = π × 20 × 20 cm2 = 400π cm2 Area of the uncut portion = (400π – 100π) cm2 = 300π cm2 Ratio of uncut to cut area = 300π : 100π = 3 : 1 Hence, answer option 3 is correct.
- CAT 1996 QA | Geometry – Mensuration CAT Question
A wooden box (open at the top) of thickness 0.5 cm, length 21 cm, width 11 cm and height 6 cm is painted on the inside. The expenses of painting ar Rs. 70. What is the rate of painting per square centimeters?
(a) Re 0.7
(b) Re 0.5
(c) Re 0.1
(d) Re 0.2
Details
Inside dimensions of cube are as follows: Length = 21 − 2 ∗ ( 0.5 ) = 20 21−2∗(0.5)=20 Width = 11 − 2 ∗ ( 0.5 ) = 10 11−2∗(0.5)=10 Height = 6 − 0.5 = 5.5 6−0.5=5.5 (As top surface is open) So total…
rea painted = 2 ( 20 × 5.5 ) + 2 ( 10 × 5.5 ) + ( 10 × 20 ) 2(20×5.5)+2(10×5.5)+(10×20) = 220 + 110 + 200 =220+110+200 = 530 =530 sq. cm. Cost of painting 530 sq. cm. is 70 So cost per sq. cm. = 70 …
So cost per sq. cm. = 70 530 = 0.1 530 70=0.1 (nearly)…
- CAT 1994 QA | Geometry – Mensuration CAT Question
A right circular cone, a right circular cylinder and a hemisphere, all have the same radius, and the heights of the cone and cylinder equal to thei diameters. Then their volumes are proportional, respectively to
(a) 1 : 3 : 1
(b) 2 : 1 : 3
(c) 3 : 2 : 1
(d) 1 : 2 : 3
Details
To find: The ratio of the volumes of the cone, cylinder, and hemisphere. Solution: Let’s assume the radius and height of the cone, cylinder, and hemisphere to be ‘r’ and ‘h’ respectively. Volume of the Cone: The volume of a cone is given by the formula Vcone = (1/3)πr²h. Given that the radius is ‘r’ and the height is ‘h’, the volume of the cone can be written as Vcone = (1/3)πr²(2r) = (2/3)πr³. Volume of the Cylinder: The volume of a cylinder is given by the formula Vcylinder = πr²h. Given that the radius is ‘r’ and the height is ‘h’, the volume of the cylinder can be written as Vcylinder = πr²(2r) = 2πr³. Volume of the Hemisphere: The volume of a hemisphere is given by the formula Vhemisphere = (2/3)πr³. Given that the radius is ‘r’, the volume of the hemisphere can be written as Vhemisphere = (2/3)πr³. Ratio of the Volumes: To find the ratio of the volumes, we can compare the volumes of the cone, cylinder, and hemisphere. Vcone : Vcylinder : Vhemisphere = (2/3)πr³ : 2πr³ : (2/3)πr³ = (2/3)πr³ : (6/3)πr³ : (2/3)πr³ = 1 : 3 : 1 Answer: Therefore, the ratio of the volumes of the cone, cylinder, and hemisphere is 1 : 3 : 1, which is option ‘A’.
- CAT 1994 QA | Geometry – Mensuration CAT Question
A right circular cone of height h is cut by a plane parallel to the base and at a distance h/3 from the base, then the volumes of the resulting cone an the frustum are in the ratio
(a) 1 : 3
(b) 8 : 19
(c) 1 : 4
(d) 1 : 7
Details
Volume of the original cone ‘V’ =πr2h3
Height of the smaller cone =2h/3
and radius =2r3(from similarΔ’s)
Voume of smaller cone
=13π(2r3)22h3=881πr2h=8V27
Volume of smaller cone Volume of frustum=8V/27V−8V/27=8:19
- CAT 1993 QA | Geometry – Mensuration CAT Question
A slab of ice 8 inches in length, 11 inches in breadth, and 2 inches thick was melted and resolidified into the form of a rod of 8 inches diameter. Th length of such a rod, in inches, is nearest to
(a) 3
(b) 3.5
(c) 4
(d) 4.5
Details
It is given that for a ice slab, length = 8 inches, breadth =11 inches and thickness(or height of slab) =2 inches,
Then the volume of this ice slab,
V1=length× breadth× height�1=length× breadth× height
=
8×11×28×11×2 cubic inches.
=176 cubic inches.
Now for the cylindrical rod, the given diameter is 8 inches,
So, radius =
dimeter2=82dimeter2=82 inches =4 inches.
And let the length(or height) of the rod be h inches.
Then the volume of this rod,
V2=π(radius)2× height�2=�(radius)2× height
V2=π×42×h�2=�×42×ℎ cubic inches.
Now from the equation (1) we can write,
V1=V2�1=�2
⇒176=π×42×h⇒176=�×42×ℎ
⇒π×16×h=176⇒�×16×ℎ=176
⇒h=176π×16⇒ℎ=176�×16
⇒h=176(227)×16⇒ℎ=176(227)×16 $$∵π=227$$$$∵�=227$$
⇒h=176×722×16⇒ℎ=176×722×16
⇒h=1232352⇒ℎ=1232352
⇒h=3.5⇒ℎ=3.5
Therefore we can say that the length of the rod is 3.5 inches.
Hence the correct option is option B.











