CAT 2022 Slot 3 Question 1-
A glass contains 500 cc of milk and a cup contains 500 cc of water. From the glass, 150 cc of milk is transferred to the cup and mixed thoroughly. Next, 150 cc of this mixture is transferred from the cup to the glass. Now, the amount of water in the glass and the amount of milk in the cup are in the ratio
A.3 : 10
B.10 : 3
C.1 : 1
D.10 : 13
Explanation

in the glass and the amount of milk in the cup will be in the ratio 1 : 1.
CAT 2022 Slot 2 Question 2-
There are two containers of the same volume, first container half-filled with sugar syrup and the second container half-filled with milk. Half the content of the first container is transferred to the second container, and then the half of this mixture is transferred back to the first container. Next, half the content of the first container is transferred back to the second container. Then the ratio of sugar syrup and milk in the second container is
A.5 : 6
B.5 : 4
C.6 : 5
D.4 : 5
Explanation
Let the half volume of each container be 80 cc.
Why 80cc though? Why not some other value?
We know that the process of shifting half volumes is happening three times overall.
(1/2)3=1/8(1/2)3=1/8.
So it would be wise to assume the initial volume to be some multiple of 8 so that we don’t have to deal with fractions later on.

CAT 2022 Slot 1 Question 3-
A mixture contains lemon juice and sugar syrup in equal proportion. If a new mixture is created by adding this mixture and sugar syrup in the ratio 1 : 3, then the ratio of lemon juice and sugar syrup in the new mixture is
A.1 : 6
B.1 : 4
C.1 : 5
D.1 : 7
Explanation
The concentration of sugar syrup in the mixture is 1/2
. (The mixture has equal quantities of lemon juice and sugar syrup)
The concentration of sugar syrup in pure sugar syrup is 1.
The initial mixture and the pure sugar syrup are mixed in a ratio 1 : 3 to form a new mixture.
That is 2 items with sugar syrup concentrations 1/2
and 1 respectively are mixed in the ratio 1 : 3 to form a new mixture. So the concentration of sugar syrup in such a new mixture is 1/2∗1+1∗3/1+3=3.5/4=7/8
The concentration of sugar syrup in the new mixture is 7/8
, that means out of 8 units of volume of the new mixture, 7 units are sugar syrup and the remaining one unit is lemon juice.
Hence the ratio of lemon juice to sugar syrup in the new mixture is 1 : 7
Alternate Approach:
We are mixing a mixture of lemon juice and sugar syrup with pure sugar syrup in a ratio 1 : 3.
That means, we mix 1 unit of this mixture with 3 units of pure sugar syrup.
This is equivalent to mixing 2 units of the mixture with 6 units of pure sugar syrup.
Mixture alternate approach 1
But what do we know about this mixture of lemon juice and sugar syrup?
We know that it contains equal quantities of lemon juice and sugar syrup. This means we can consider two units of this mixture as a unit each of lemon juice and sugar syrup.
Mixture alternate approach 2
Clearly, the new mixture contains one unit of lemon juice and 7 units of sugar syrup.
Hence, the ratio of lemon juice to sugar syrup in the new mixture is 1 : 7
CAT 2021 Slot 3 Question 4-
If a certain weight of an alloy of silver and copper is mixed with 3 kg of pure silver, the resulting alloy will have 90% silver by weight. If the same weight of the initial alloy is mixed with 2 kg of another alloy which has 90% silver by weight, the resulting alloy will have 84% silver by weight. Then, the weight of the initial alloy, in kg, is
A.3
B.2.5
C.4
D.3.5
Explanation

CAT 2021 Slot 2 Question 5- From a container filled with milk, 9 litres of milk are drawn and replaced with water. Next, from the same container, 9 litres are drawn and again replaced with water. If the volumes of milk and water in the container are now in the ratio of 16 : 9, then the capacity of the container, in litres, is
Explanation

CAT 2021 Slot 1 Question 6-
The strength of an indigo solution in percentage is equal to the amount of indigo in grams per 100 cc of water. Two 800 cc bottles are filled with indigo solutions of strengths 33% and 17%, respectively. A part of the solution from the first bottle is thrown away and replaced by an equal volume of the solution from the second bottle. If the strength of the indigo solution in the first bottle has now changed to 21% then the volume, in cc, of the solution left in the second bottle is
Explanation

CAT 2020 Slot 3 Question 7-
Two alcohol solutions, A and B, are mixed in the proportion 1:3 by volume. The volume of the mixture is then doubled by adding solution A such that the resulting mixture has 72% alcohol. If solution A has 60% alcohol, then the percentage of alcohol in solution B is
A.94%
B.92%
C.90%
D.89%
Explanation
We are told that the A and B are mixed in the ratio 1:3
That means, one unit of A is mixed with 3 units of B
Observe that the total Volume is 1 + 3 = 4 units.
The volume is doubled by adding A, this implies that a quantity of 4 units of A is added to the existing 4units of the mixture.
The total volume will now be 4 + 4 = 8 units.
Of which three units are B and the rest 5 units are A. Hence the ratio of A to B in the final mixture is 5 : 3
We are told that A has a concentration of 60% alcohol and the final mixture has a concentration of 72% alcohol
Therefore, 5×ConcentrationofA+3×ConcentrationofB/5+3 = 72
5×60+3×ConcentrationofB/5+3 = 72
300+3×ConcentrationofB/8 = 72
300 + 3 × Concentration of B = 576
3 × Concentration of B = 576 – 300 = 276
3 × Concentration of B = 276 = 270 + 6
3 × Concentration of B = 270 + 6
Concentration of B = 270/3
+ 6/3
Concentration of B = 90 + 2 = 92.
CAT 2020 Slot 1 Question 8-
An alloy is prepared by mixing metals A, B, C in the proportion 3 : 4 : 7 by volume. Weights of the same volume of metals A, B, C are in the ratio 5 : 2 : 6. In 130 kg of the alloy, the weight, in kg, of the metal C is
A.84
B.48
C.96
D.70
Explanation
A : B : C
3 : 4 : 7 (Volume)
5 : 2 : 6 (1L of each)
15 : 8 : 42 (Total)
Totally 65kg
Asked in 130 kg C’s weightage
In 65 kg C’s weight = 42kg, So in 130kg C’s weightage = 84kg
CAT 2019 Slot 2 Question 9-
The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is
A.15
B.12
C.13
D.14
Explanation
Vessels A, B and C contains salt solution of strengths 10%, 22% and 32% respectively
It is also given that the amount of salt solution = 500 ml
So, Vessels A, B and C contains salt of 50 grams, 110 grams and 160 grams respectively
100 ml of Solution is transferred from A to B:
A would have 400 ml, B would have 600 ml of solution
Amount salt from A which is transferred to B = = 10 grams
So, Total salt in B = 110 + 10 = 120 grams (After first transfer)
Total salt in A = 40 grams (After first transfer)
Now, 100 ml from Vessel B is transferred to Vessel C
So similarly, of salt would transfer from B to C
Total Salt in B = 120 – 20 = 100 grams (After second transfer)
Total Salt in C = 160 + 20 = 180 grams (After second transfer)
Now, 100 ml from Vessel C is transferred to Vessel A
So similarly, of salt would transfer from C to A
Total Salt in C = 160 – 30 = 130 grams (After third transfer)
Total Salt in A = 40 + 30 = 70 grams (After third transfer)
So, Vessel A contains 70 grams Salt in 500 ml solution
Strength of Salt Solution in Vessel A = 14%
CAT 2019 Slot 1 Question 10-
A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is
A.70
B.85
C.80
D.75
Explanation
In Liquid L1 – 1L = 1000 grams
So, 1000 mL = 1000 grams
1 mL = 1 gram
x mL = x grams
In Liquid L2 – 1L = 800 grams
1000 mL = 800 grams
1mL = 0.8 grams
(500-x) mL = (500-x) x 0.8 grams
Total mass = x + 400 – 0.8x = 480 grams
0.2x = 80 grams
x = 400 grams
Therefore, Liquid 1 has 400 mL and Liquid 2 has 500 – 400 = 100 Ml
Therefore, Percentage of Liquid 1 = x 100 = 80%
CAT 2018 Slot 2 Question 11-
A 20% ethanol solution is mixed with another ethanol solution, say, S of unknown concentration in the proportion 1:3 by volume. This mixture is then mixed with an equal volume of 20% ethanol solution. If the resultant mixture is a 31.25% ethanol solution, then the unknown concentration of S is
A.50%
B.55%
C.48%
D.52%
Explanation

Here to find the solution, do the second thing first and then go to the first thing
The second one is mixed in the ratio 1 : 1 so that the final thing should be bang in the middle
The question is “A 20% ethanol solution is mixed with another ethanol solution, say, S of unknown concentration in the proportion 1:3 by volume. This mixture is then mixed with an equal volume of 20% ethanol solution. If the resultant mixture is a 31.25% ethanol solution, then the unknown concentration of S is”
Hence, the answer is 50%
CAT 2018 Slot 2 Question 12-
A jar contains a mixture of 175 ml water and 700 ml alcohol. Gopal takes out 10% of the mixture and substitutes it by water of the same amount. The process is repeated once again. The percentage of water in the mixture is now
A.25.4
B.20.5
C.30.3
D.35.2
Explanation
Given that a jar contains a mixture of 175 ml water and 700 ml alcohol.
It is given that 10% of the mixture is removed and it is substituted by water of the same amount and the process is repeated once again
Now we have to find the percentage of water in the mixture.
Since the mixture is removed and substituted with water, we can deal with alcohol and the second step we can find how much amount of alcohol is retained and not about how much amount of alcohol is removed
As 10% of alcohol is removed, 90% of alcohol is retained
So alcohol remaining = 700 × 90% × 90%
⟹ 700 × 0.9 × 0.9 = 567
We totally have 875 ml overall mixture and of this 567 ml is alcohol.
Remaining 875 – 567 = 308 is the amount of water.
We have to find the percentage of water in the mixture i.e. 308875
Approximately 308 is 30% of 1000 so by this we know that 308 is more than 30%
Hence 35.2% is the percentage of water in the given mixture.
The question is “A jar contains a mixture of 175 ml water and 700 ml alcohol. Gopal takes out 10% of the mixture and substitutes it by water of the same amount. The process is repeated once again. The percentage of water in the mixture is now”
Hence, the answer is 35.2%
CAT 2018 Slot 2 Question 13-
The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. If three salt solutions A, B, C are mixed in the proportion 1 : 2 : 3, then the resulting solution has strength 20%. If instead the proportion is 3 : 2 : 1, then the resulting solution has strength 30%. A fourth solution, D, is produced by mixing B and C in the ratio 2 : 7. The ratio of the strength of D to that of A is
A.3 : 10
B.1 : 3
C.2 : 5
D.1 : 4
Explanation

CAT 2018 Slot 1 Question 14-
A trader sells 10 litres of a mixture of paints A and B, where the amount of B in the mixture does not exceed that of A. The cost of paint A per litre is Rs. 8 more than that of paint B. If the trader sells the entire mixture for Rs. 264 and makes a profit of 10%, then the highest possible cost of paint B, in Rs. per litre, is
A.20
B.16
C.22
D.26
Explanation
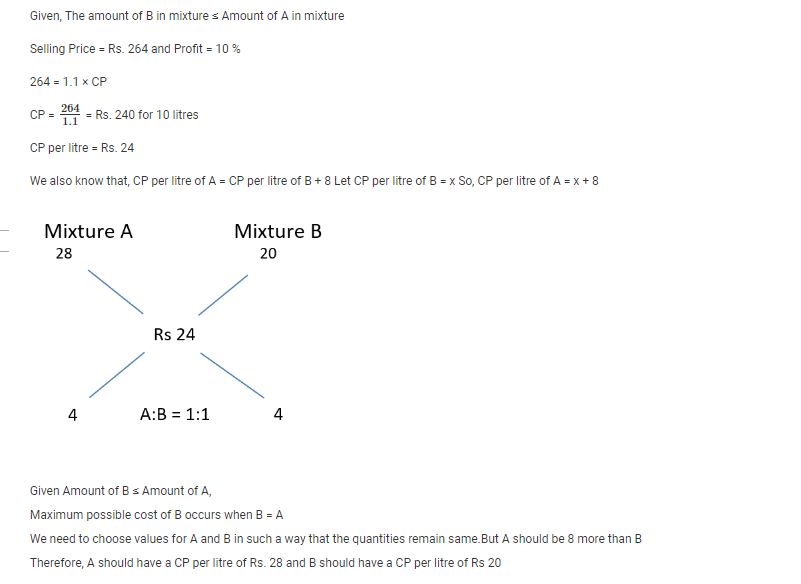
B cannot be assigned any more than this as the amount of B would become more than A
Example: Let us assign B to be Rs. 21 and A to be Rs. 29 which would result in a ratio of 3:5 where B amounts more than A, which doesn’t satisfy the condition
Max possible cost of Paint B = Rs. 20 per litre
CAT 2017 Slot 2 Question 15 –
Bottle 1 contains a mixture of milk and water in 7 : 2 ratio and Bottle 2 contains a mixture of milk and water in 9 : 4 ratio. In what ratio of volumes should the liquids in Bottle 1 and Bottle 2 be combined to obtain a mixture of milk and water in 3 : 1 ratio?
A.27 : 14
B.27 : 13
C.27 : 16
D.27 : 18
Explanation
Bottle 1 and bottle 2 contains mixture of milk and water in the ratio 7 : 2 and 9 : 4 respectively.
We have to find by what ratio bottle 1 and Bottle 2 should be combined to obtain a mixture of milk and water in the ratio 3 : 1
For this we can consider milk to the whole mixture or else water to the whole mixture.
⟹ 7/9 – 3/4
Taking LCM we get 28−27/36 = 1/36
⟹ 3/4- 9/13
LCM is 52 so 39−36/52 = 3/52
3/52 : 1/36
⟹ 3/52
× 36./1
= 27 : 13
Bottle 1 and 2 are mixed in the ratio 27 : 13











